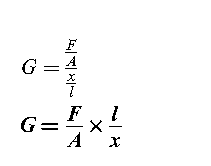Fastenings
Engineering fastenings such as rivets, bolts, the different kinds of
machine screws and setscrews, self-tapping screws and hinge pins are
frequently subjected to shear loading. Shear loading occurs when
equal and opposite parallel forces act on a component. Direct loading
tends to cause failure perpendicular to the direction of loading
whereas shear loading tends to cause failure parallel to the direction
of loading. Direct loading and its effects have already been dealt with
(and we will now examine the effects of shear loading (Figure 1.54
Shear stress
Shear stress , is a measure of the intensity of loading over the
sheared area A.
Shearing forces tend to distort the shape of a component as shown
in Figure 1.55.
Shear strain , is a measure of the deformation which the
shearing force produces. It is the ratio of the displacement of the
sheared surfaces to the distance between them.
The angle , is called the angle of shear. Its tangent is equal to the
shear strain
(Shear modulus or (Modulus of rigidity
When an elastic material is subjected to shear loading, the displacement
x of the sheared surfaces is proportional to the load F,
which is applied. Also the shear stress is proportional to the
shear strain .
A graph of shear stress against shear strain is a straight line, as
shown in Figure 1.56, whose gradient for a given material is always
found to be the same. It gives a measure of the elasticity or
‘stiffness’ of the material in shear and is known as its Shear
Modulus, G. In older text books you might find that it is called
the Modulus of Rigidity
Substituting the expressions for shear stress and shear strain from
equations previous
It will be noted that several of the above formulae are similar to those
derived for direct stress and strain and theModulus of Elasticity but
they should not be confused. The symbols F, A, l and x have different
meanings when used to calculate shear stress, shear strain and shear
modulus. Furthermore, the values of Modulus of Elasticity E, and
ShearModulus G, are not the same for any given material. With mild
steel, for example, E=210GNm 2 whilst G=85GNm 2